Q. Please tell me about metastables
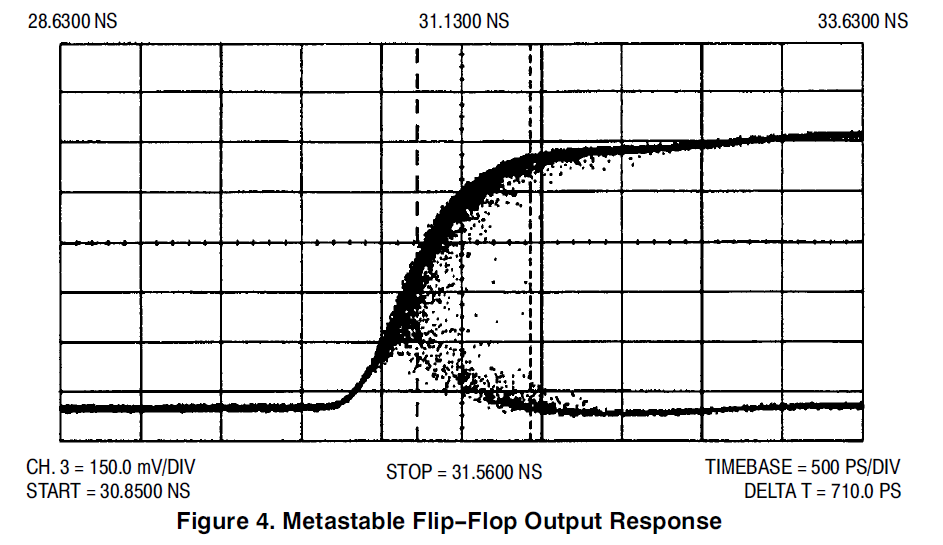
Introduction: Any asynchronous input from the outside world to a clocked circuit represents a source of unreliability, since there is always some residual probability that the clocked circuit will sample the asynchronous signal just at the time that it is changing. From a specification point of view, synchronous elements such as flip flops specify a Setup time and a Hold time. By its nature an asynchronous input cannot be reliably expected to meet this specification, and so it will have transitions that fall within the timing window that is bounded by these two specifications. When this occurs, the result can be one of three scenarios: 1) The state of the signal prior to the transition is used. 2) The state of the signal after the transition is used. 3) The flip flop goes metastable. The first two possibilities are of no consequence, since the signal is asynchronous, but the third possibility is what the rest of this article is about. Metastability caused havoc in synchronous systems. It is caused by the unstable equilibrium state for example when a pair of cross coupled CMOS inverters are stuck at mid-voltages. It is impossible to determine how long such a state persists. Unfortunately, due to the complexities in today's systems, it is not possible for the designer to avoid this type of situation. The most common approach to minimizing the problems of metastability propagating into our synchronous systems is to use a synchronizing circuit to take the asynchronous input signal, and align it to the timing regimen of the rest of the system. The synchronizer though can go metastable itself, and the goal of a designer is to minimize the probability of this occuring and propagating to the output of the synchronizer. In current (2004) technology, this can usually be achieved with a two stage or three stage synchronizer. Far more details follow in this article. A. This is an informational (I hope) posting, hopefully giving some additional insight to the behavior of metastables. Some nice updates from September 2001 that address the issues of simulating designs. The following is an edited version of some of my postings to sci.electronics.design, during May of 2000. Since this is quite long, here is a quick guide to the contents of this message: 1) The original poster asked people to look at his WWW page, where he had a schematic for a claimed metastable free design. Several people pointed out his error, including me. My response includes some historical notes, as well as a list of observed metastable behavior. The original poster never responded. 2) Another poster also responded, and assumed that metastables only occur as an oscillation (a pulse running around a loop). My response details the internal mechanism for metastables, and also discusses some old TTL technology. 3) The poster in (2) followed up my post, and I replied again. In this post, we discussed oscillation versus delayed output. I made my case that I believe at the system level, both are just as bad, and so tricks that convert an oscillation metastable into a delayed output metastable are of no use. In particular, I comment that the signals that we are worried about going metastable are signals that connect to the D pin of flip-flops. As such, oscillation or delayed transition are both a disaster. Signetics (a division of Philips (no relation)) used to claim they had a metastable immune flip-flop. The 74F50109 description includes the following: " The 74F50109 is designed so that the outputs can never display a metastable state due to setup and hold time violations. If setup and hold times are violated the propagation delays may be extended beyond the specifications but the outputs will not glitch or display a metastable state. Typical metastability parameters for the 74F50109 are: t < .2 ns, T0 = 10us, and h=3.8 ns." Absolutely incredible! The names have been changed to protect the lack of an NDA. >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> Hi XXXX, I've seen two posting that both describe the path that shows that when fdiv_2 is low, the async signal goes all the way through to the final flipflop. The topic of designing circuits for dealing with metastability is a very well researched area. The now widely held belief is that it is impossible to design such a circuit. Indeed, ALL claimed metastable free circuits have been proven not to be. Usually the only thing achieved by complex circuits that try and deal with all sorts of special cases, is that they obscure the metastable mode during analysis. The best way to deal with the metastable problem (the synchronization of an asynchronous signal feeding into and affecting a synchronous system) is to synchronize the signal with a multi stage synchronizer, comprizing of no more than 2 or more flipflops, connected as a shift register, and clocked by the clock of the destination domain. Even such circuits as a three stage synchronizer, with the first and third flipflop clocked on the rising edge of the clock and the middle flipflop clocked on the falling edge, are less effective than a simpler two stage synchronizer, with both clocked on the rising edge. While much of the really good literature on the topic has been written by Fred Rosenberger and Thomas Chaney, as early as 1966 , many others have also written on the topic. B. I. Strom of Bell Labs wrote in 1979 "Proof of the equivalent realizability of a time-bounded arbiter and a runt-free inertial delay" Which basically shows that both are un-realizable. The guts of an arbiter is the desired metastable-free flipflop. In 1977, E. G. Wormald published a note in the IEEE transactions on computing, march 1977, page 317, claiming to have designed a metastable free flipflop. At the core of the design, it used a Schmitt trigger to try and avoid metastability. In IEEE trans. on comp. Oct 1979, page 802, Thomas Chaney commented on the Wormald design. He explained that Schmitt triggers can them selves go metastable. He built a circuit as per Wormald'd note, and demonstrated that it went metastable. He closed with the following: "In closing, there is a great deal of theoretical and experimental evidence that a region of anomalous behavior exists for every device that has two stable states. The maturity of this topic is now such that papers making contrary claims without theoretical or experimental support should not be accepted for publication". Wormald's response to Chaney (same issue) includes the following: "Hopefully, the discussion will discourage further attempts to eliminate this unavoidable characteristic" While your design does not use Schmitt triggers, it has been shown that there is a path that allows the asynch signal to feed the final flip flop, and therefore it can go metastable. Unfortunately, simulation is NOT sufficient proof of metastable free behavior. For a good example of someone who has fooled themself (and the patent office) see 4,999,528 . Spice does not have infinite precision, and the problems of rounding and convergence are well known. Also let me state that there are a few lost souls who think that the only way a metastable presents itself is as an oscillation on the output. This is not the case. Metastable outputs can be 1) Oscillations from Voh to Vol, that eventually stop. 2) Oscillations that occur (and may not even cross) Voh and Vol 3) A stable signal between Voh and Vol, that eventually resolves. 4) A signal that transitions to the opposite state of the pre clock state, and then some time later (without a clock edge) transitions back to the original state. 5) A signal that transitions to the oposite state later than the specified clock-to-output delay. 6) Probably some more that I haven't remembered. I would suggest a change in the title of your web page :-) >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> YYYY posted the following (indented by ">"), and I responded >I have thought about this problem for a while. The point that becomes >clear is that any digital solution simply moves the hazard to the next >level. I agree. >I think there may well be a solution, but it lies with the analog >behavior of the gates in use, and related to stability criteria used in >feedback theory. I totally disagree (sorry), see my article above. >Think of a D flip-flop as two cascaded latches, open alternately on the >clock high and low state. > >First of all, the latches must have mux hazard protection: > > Q = (D & LE) # (Q & !LE) # (D & Q); > >Logic compilers typically throw away the last term as "redundant", but >in reality !(LE) != !LE , so it's not redundant. !LE is inverted AND >DELAYED from LE, or the other way around. > >Next, the latch loop gain must meet stability criteria. If the latch >loop delay is more than about half the slew time, there is a hazard of >metastability. Metastability is when the a latch feedback loop thrashes >on and off, chasing itself. That's only one of it's failure modes. Another is when the loop assumes an (almost stable) analog level between the two normal '1' and '0' states. Here's how it fails. The latch, when closed effectively comprises two inverters in a loop. If the input to the first is '0', its output is '1', and there fore the output of the second inverter is '0', which was driving the input of the first inverter. It is therfore latching the value. The opposite state is also possible. To load the latch, the loop is opened, and a '0' or a '1' is connected to the input of the first inverter. The output of the second inverter will with time become the same level, and when the loop is closed, the output of the second inverter is reconnected to the input of the first. The inverters are basically high gain inverting amplifiers. If you apply an analog signal to the input, there is a region of the input range for which the output is a value other than the desired '0' or '1' levels. For example, lets have an inverter running at 5V, with rail to rail outputs, and the middle of its switching theshold is 2.0V, and it has a gain of 20. (for simplicity I will assume a linear monotonic transfer characteristic for the analog region) INPUT OUTPUT 0 5 1 5 1.8 5 1.9 4.5 1.95 3.5 2.0 2.5 2.01 2.3 2.02 2.1 2.025 2.0 2.03 1.9 2.04 1.7 2.05 1.5 2.1 0.5 2.2 0 3 0 4 0 5 0 Somewhere between 2.02 and 2.025 volts input, the output will be the same value. I leave it as an exercise for the reader to determine the value. Ok, it is approximately 2.02380952380952 If I have two such inverters in series, and the output of the second is connected to the input of the first, then the loop will be stable (for some time) at this intermediate value. Even if the two inverters are not identical, there is still some analog value that when placed on the input of the first inverter, will cause an output which when fed to the second inverter will cause its output to assume a value that matches the input to the first inverter. This is true of ALL bistable circuits. The loop does not need to be made of inverters. This is independent of the loop gain (other than it must be greater than 1). This is independent of loop delay. How does this analog level get into our "digital" systems? Take a step back and think about the way the latch is made to "track" the input signal, while the latch is open. The loop is opened, and the input signal charges and discharges the input node of the first inverter. The charging and discharging depends on the size of the capacitance of the node, and the impedance of the input signal source and the interconnect to the first inverter. The input can not instantaneously change from the '0' to '1' levels. It must transition through the analog region where the output is transitioning through its analog region. See the table above. The charging stops and the loop is closed when the clock signal transitions. If this happens at just the wrong time, the value on the input of our first inverter meets the criterion for the loop to be in the metastable state, of being neither a '0' or a '1'. The quality of a device to minimize how often it goes metastable, and how long it may stay that way depends on the loop gain, and the signal transition rates. Improving both these characteristics will minimize the region for which the inputs and outputs are in the analog region. >If the loop delay is 10nS, a 5nS pulse can race around the loop until >slew asymmetry wipes out one side of the wave. This is why TTL, which is >highly asymmetric, is "less prone" to metastability. In fact, such >storms in TTL logic simply move quickly to a "0" because the pull down >is always a lot stronger than the pull up. Unfortunately, this is not true either. Since there are two gates in the loop, even if you did have a pulse racing around the loop, what one gate would make shorter, the other gate would make longer. One of the worst devices for metastability is the 74S74. Almost all other 74xxx74 devices behave better. Your assertion that TTL quickly resolve to '0' is also incorrect. A device in a metastable condition has equal likelihood of resolving to a '0' or a '1'. > >In analog terms, a "single dominant pole" in the latch feedback should >mean that the latch will produce, at worst, a single pulse, if any. See below for a list of the ways that a metastable can be seen. >If the second latch of the DFF is not open for some delay after the >closure of the first, then this pulse is not seen at the DFF output. Unfortunately, the duration of the metastable state in the first latch is unbounded, and so there is no guarantee that it will be resolved by the time the second latch is opened. Delaying the opening of the second latch cannot guarantee hiding the metastability, and would also adversely affect the clock to output time of the circuit. >The >second latch must also close before the first opens (on the falling >clock), ie: > >LE1= !clock & !LE2; >LE2= clock & !LE1; > >A latch uses positive feedback, not negative, but you can see that if >the loop gain is high at the frequency = 1/loop_delay, wrt DC gain, the >latch can oscillate for a time before stabilizing. >Cheers, >YYYY Sorry for the bad news YYYY, Cheers anyway :-) Philip >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> YYYY responded (indented by ">") and I replied: >I was thinking that it might be possible for a circuit to meta-stabilize >faster than the general response, and so hiding the problem, but as you >point out the meta-unstable time can be unbounded. > >A couple ideas: > >1. If the failing loop is followed by a third gate who's threshold is >off from the point of equilibrium, then this static condition becomes a >1 or 0. For this reason, I think, in many cases, a static failure mode >does not translate to the kinds of system failure that oscillating does. >This leaves us with the dynamic case I was interested in. A strategy >aimed at damping oscillation would be useful, even if it does nothing >for the static case. > >Cheers, >Steve Although oscillation and delayed transition are two of the several ways a metastable can manifest itself (see my previous article for some other failure modes), what you are suggesting above will basically turn the oscillation mode into the delayed output mode. ( In fact, I suspect this is what actually happens in the delayed output case, or something similar. Here are two scenarios: a) Internal latch oscillates with a small swing. The output of the latch is buffered, and the buffer has a threshold that is outside of the peak to peak swing of the oscillation. When the oscillation stops, and the latch takes on a stable '1' or '0' state, the following buffer then 'reports' the result, but with late clk-to-q problem. b) Internal latch oscillates with large swing. The output of the latch is buffered, and the buffer is slow (or is slowed by its load), and the high frequency oscillations dont get seen on the buffer's output. When the oscillation stops, and the latch takes on a stable '1' or '0' state, the following buffer then 'reports' the result, but with late clk-to-q problem. ) While you characterize the oscillating and delayed outputs as two different failure modes (you call them dynamic and static), to me they are the same thing: The flipflop does not behave as per the data sheet, and valid Q is late. Here's some info about my digital design style which may help to understand my position: I do digital design that is fully synchronous. ALL flipflops are clocked by one master clock signal. Clocks are never gated. Async reset or set are only used for system initialization. Clock enables (mux in D path, recirculating Q ) for flipflops that need to have their clock disabled for some cycles. Async inputs are handled in carefully designed circuits that minimize the occurence of metastables getting into the main design. From a timing point of view, all async paths within the design start at a flipflop, go through some cloud of logic, and end at a flipflop. Since all flops are clocked by the same clock signal, all logic paths have the same worstcase delay requirements, which is clock period minus flipflop output time minus flipflop setup time. This can be exhaustively analyzed by a static timing analyzer. The design only needs functional (unit delay) simulation, and timing simulation is un-needed. If the system must have more than 1 master clock, i.e. data arrives from a source with a 50MHz clock, and is processed and leaves with a 27.5MHz clock, then I break the design into two sub-designs, that are each totally synchronous, and great care is applied at the point where the data moves between the two domains. FIFOs, dual port memories, semaphores/flags, and carefully designed synchronizers all help to cross the chasm. So in my systems, the signals that can go metastable, are signals that in the limit always have D pins as their destinations. Never clock pins. So whether it oscillate and then goes stable, or just goes to a stable state at a later time, it is still violating the clock-to-Q spec of the data sheet, and this value was used to guarantee system timing during static timing analysis. I am unable to imagine a scenario where a signal that could go metastable is used as a clock to a flipflop, and where the difference between oscillating or delayed signal would make a difference. ============================================================================= Update: 2001/06/03 I have had some discussions with the author of the following page, and you may find it useful too. It has some good diagrams and graphs. Design_MetaStable ============================================================================= Update: 2001/09/29 There was an interesting discussion about how simulators show (or fail to show) the effects of metastability The thread started with a question by Manjunathan, who had designed a circuit with a 3 stage synchronizer, but was having trouble simulating it: I have a doubt in transfering a signal from one clock(clka) to another(clkb). Below I have explained in detail. I have registered the signal three times, in clockB domain, after that I have used this signal. Since, there is a chance of metastablility in the flipflop one, to avoid this I have registered again two times more. But when i implemented this desgin, and simulated the deign with SDF in MODEL-TECH. Here the flip flop one, goes to metastability, and this unknown value propagates to second and the third one also. My question is that does this design works in real time? even though it fails during simulation ? Can you give me a suggestion to avoid metastability? How to prevent the propagation of the unknown? Here is his VHDL code library IEEE; use IEEE.std_logic_1164.all; entity check_meta_stability is port ( clk1: in STD_LOGIC; clk2: in STD_LOGIC; reset1: in STD_LOGIC; reset2: in STD_LOGIC; o: out STD_LOGIC ); end check_meta_stability ; architecture check_meta_stability_arch of check_meta_stability is signal s1,s2,s3 : std_logic; begin process (clk1,reset1) begin if reset1='1' then s1 <= '0' ; elsif clk1='1' and clk1'event then s1 <= not s1 ; end if ; end process ; process (clk2,reset2) begin if reset2='1' then s2 <= '0' ; s3 <= '0' ; o <= '0' ; elsif clk2='1' and clk2'event then s2 <= s1 ; s3 <= s2 ; o <= s3 ; end if ; end process ; end check_meta_stability_arch; Here is my response to his questions: Your approach to minimizing the probability of metastability in your system is the correct approach, and a 3 stage synchronizer is about as much as anyone is likely to use. There are several articles that Xilinx has published in their data books and XCELL magazine that give details of the probability calculations, and the raw data for the components that is needed to do the calculations. Unfortunately, the data for components only covers older technology. On the bright side, all the current components are almost certainly better in terms of probability of going metastable, and probable duration to resolution. But now, on to your question. As it turns out, you are not simulating metastability. I know of no digital simulator that can simulate metastability. What you are simulating is a setup/hold violation. Your flip-flop model is taking the violation, and setting the Q output to X. This then propagates through your simulation, which is what you are seeing. There is no probability calculation going on, which is why your simulation is probably showing the problem propagating through the 3rd flip-flop all the time. Depending on your clock rate, etc, the reality is it might propagate once in every 10^-20 times or maybe 10^-50 it depends on many things, but is far more rare than your simulation is showing. You can't fix your simulation to show the correct rate, because it is so rare, you would be simulating for ever before you saw a metastability. The correct analysis is to do the calculations. As for your simulation, once you have done your calculations, and confirmed that the 3 stage synchronizer reduces the probability of metastability sufficently, you should proceed with simulation, as if the metastabilities do not come out of the third flip flop. You can then check the rest of your design. So in answer to your question: "my question is that does this design works in real time? even though it fails during simulation ?" is "yes", provided you don't have other logic errors. You also asked "how to prevent the propagation of the unknown?" As for making the simulation make more sense, what you need to do is any of a) adjust clkA so that in simulation you don't get the setup/hold violations or b) Figure out how to disable setup/hold checks for just the first FF of your synchronizer or c) edit the SDF for just the first FF, and set the setup and hold times to really small values, like 1 pS or d) Add an AND gate after the first FF (only in the simulation version of the design) and drive the other input of the AND gate directly from the test bench. Run your simulation, see when the setup/hold violation occur, and adjust the test bench to mask these by blocking them at the AND gate. This was followed by another article by Brian Philofsky of Xilinx, and it gives some excellent additional info on how to change the way the simulator handles setup/hold checks. Here it is: First off in the physical realm, for most practical purposes, a two stage synchronizer would suffice for most as the chances of one register having a metastable resolution time the exact amount of time that it would take for the next register to have another metastable event occur is pretty slim. However since registers are pretty much for free in most FPGA architectures and if the added latency is not an issue, the third stage will push you closer to the impossibility of metastability ever effecting your circuit however that possibility will always exist. One thing I can suggest is to put a tighter timing constraint on the second and third stages of your synchronizing registers. By reducing the traveling time for signals in between the registers, you increase the settling time for the registers and since most metastable events settle fairly quickly, you further reduce the chance of having metastability on the second or third register stage in your synchronizer. (Editors note: Excellent advise about changing time specs for the P&R sw) Now on the simulation side of things, as mentioned there are no simulation models from any vendor (that I am aware of) that can accurately simulate metastability. To build such a model that will accurately predict the settling times for registers will to say the least be extremely difficult. So most vendors take the easy way out and output an 'X' symbolizing "we do not know what the output will be (1, 0 or something in between) for now but will resolve on the next clock cycle if another violation does not occur." As you could see, this can halt most simulations at that point and make functional verification of the design with timing not work. If your intent is to see exactly what your circuit will do if a metastable event occurs in the simulator, that currently is not possible. If however you want to verify the functionality of your circuit and do not want a setup/hold violation to halt your simulation, there are way to do this other than what has already been mentioned. In other words, you do not have to modify your stimulus or design to avoid setup violations in order to simulate as this does not always make sense (perhaps you are crossing clock domains where the clocking frequencies do not allow this for example). If you are targeting the Xilinx architectures, there is a switch in the VHDL netlister, ngd2vhdl, called -xon. If you specify the -xon switch to the false, then the simulation model produced will not go to 'X' when a setup or hold violation occurs and instead will keep its previous value. Now the thing to realize here is that the value may have very well changed in real silicon depending on when in the setup/hold window the violation occurred so this result has to be analyzed with caution however it does allow the simulation to continue without requiring you to modify your stimulus or design. For you Verilog people out there, the equivalent to this is to run the simulation with the "+no_notifier " option when invoking the simulation. Now I do not suggest to use these switches to get around timing violations from synchronous elements as it is far better to fix the timing problems than ignore them however in situations where you know you have an asynchronous path, still wish to simulate the design without setup violations stopping you and you realize that the output from the violated register may not be entirely accurate in that situation, then this is a useful to know. ============================================================================= Philip Freidin 2002/06/28 Brad Hutchings of BYU JHDL fame pointed me to this rather interesting article that gives some historic perspective on the problem. http://research.microsoft.com/users/lamport/pubs/buridan.pdf Thanks, Brad, an interesting read. (so metastability has been written about since the 14th century) ============================================================================= Philip Freidin 9/1/2003 The following is a pair of postings I made to comp.arch.fpga recently. 8/27/2003 Let me be dogmatic: Flip flops may go metastable when input signals do not meet the setup and hold specifications with regard to the clock signal. These inputs include D, CE, CLR, PRE, S, R, T, J, K. There is no cure for metastability. What you can do is trade latency of your system for higher MTBF. People that have found a cure are wrong. Circuits that purport to solve metastability through hysteresis fail because the hysteresis circuit itself can go metastable Circuits that purport to solve metastability with injected noise fail because the noise is as likely to push a non-metastable event into being a metastable event as it is to helping to resolve such an event. Just because current flip flops are better than stuff of a few years ago, and the probability and resolution time of metastable events is better, does not mean you can ignore this stuff. If someone says that things are so good now that "you almost don't have to worry about this anymore", what it means is that you absolutely need to understand it and design for it. If you don't, you will have unreliable systems. Nothing improves the MTBF of a metastable synchronizer better than just waiting longer. Not clocking the intermediate signal on the negative clock edge. Not voting. Not threshold testing. Not adding noise. Not fancy SPICE simulations. Not predicting circuits. Not circuits designed to bias the outcome to either 1 or 0. Not clocking it twice as fast through twice as many flip flops. Nothing. From Thomas Cheney, October 1979: "In closing, there is a great deal of theoretical and experimental evidence that a region of anomalous behavior exists for every device that has two stable states. The maturity of this topic is now such that papers making contrary claims without theoretical or experimental support should not be accepted for publication". 9/1/2003 > symon_ZZZbrewer@YYYhotmail.com (Symon) wrote: >Hi, > Before I start, metastability is like death and taxes, >unavoidable! That said, I've read the latest metastability thread. I >thought these points were interesting. > >Firstly, A quote from Peter, who has carried out a most thorough >experimental investigation :- >"I have never seen strange levels or oscillations ( well, 25 years ago >we had TTL oscillations). Metastability just affects the delay on the >Q output." > > >Secondly, from Philip's excellent FAQ :- Thanks. >"Metastable outputs can be > >1) Oscillations from Voh to Vol, that eventually stop. >2) Oscillations that occur (and may not even cross) Voh and Vol >3) A stable signal between Voh and Vol, that eventually resolves. >4) A signal that transitions to the opposite state of the pre > clock state, and then some time later (without a clock edge) > transitions back to the original state. >5) A signal that transitions to the oposite state later than the > specified clock-to-output delay. >6) Probably some more that I haven't remembered. " > > So, this got me thinking on the best way to mitigate the effects of >metastability. If Peter is correct in his analysis of his experimental >data, and I've no reason to doubt this, then Philip's option 5) is the >form of metastability appearing in Peter's Xilinx FPGA experiments. Peter's experimental data revolves around detecting metastables, and counting them to create the data we use for our calculations. Very good stuff! I too have created metastability test systems, which not only count the metastables, but also display them on an osciloscope. I would like to make a very strong distinction about the typically presented scope pictures of metastability, and the data that I have taken. What you normally see published (in terms of scope photos, as opposed to drawn diagrams) is a screen of dots representing samples of the Q output. These scopes are high bandwidth sampling scopes that typically take 1 sample per sweep, and rely on the signal being repetitive to build up a picture of what is going on. Examples are the Tek 11801 and 11803, as well as the newer TDS7000 and TDS8000 . The TDS8000 and CSA8000 are basically the same scopes with some extra software. The picture at the top of page 3 of this document is typical: OnSemi Appnote AN1504-D (PDF) (It is the second picture at the top of this FAQ page) The scope is triggered by the same clock as the clock to the device under test (DUT), and the scope takes a random sample (or maybe a few samples) over the duration of the sweep. Most sweeps are of the flip flop not going metastable, and so the dots accumulate and show the trajectory of the flip flop. Occasionally the flip flop goes metastable, and sometimes the random sample occurs during the metastable time. These show up as the dots that are to the right of the solid rising edge on the left. Every dot that is not on that left edge represents times when the flip flop had a longer than normal transition time, after you take into consideration clock jitter, data output jitter, scope trigger jitter, and scope sweep jitter. All of these can be characterized by first doing a test run that does not violate the setup and hold times of the DUT. The problem with these test systems is that when you do record a metastable event, you only get 1 sample point on the trajectory and you can say very little about the trajectory, other than it passed through that point. Even when these scopes take multiple samples per sweep, they are often microseconds apart, and of little interest in the domain we are talking about here. Although the collected data is predominantly of non metastable transitions, these all pile up on top of each other as the left edge of the trace, and do not significantly detract from seeing the more interesting dots to the right. The test systems that I have designed are quite different. These test systems only collect trajectory data when the flip flop goes metastable, and they sample the DUT output at 1GSamples per second, thus taking a sample every nanosecond. The result is that the scope pictures I have show the actual trajectory of the metastable.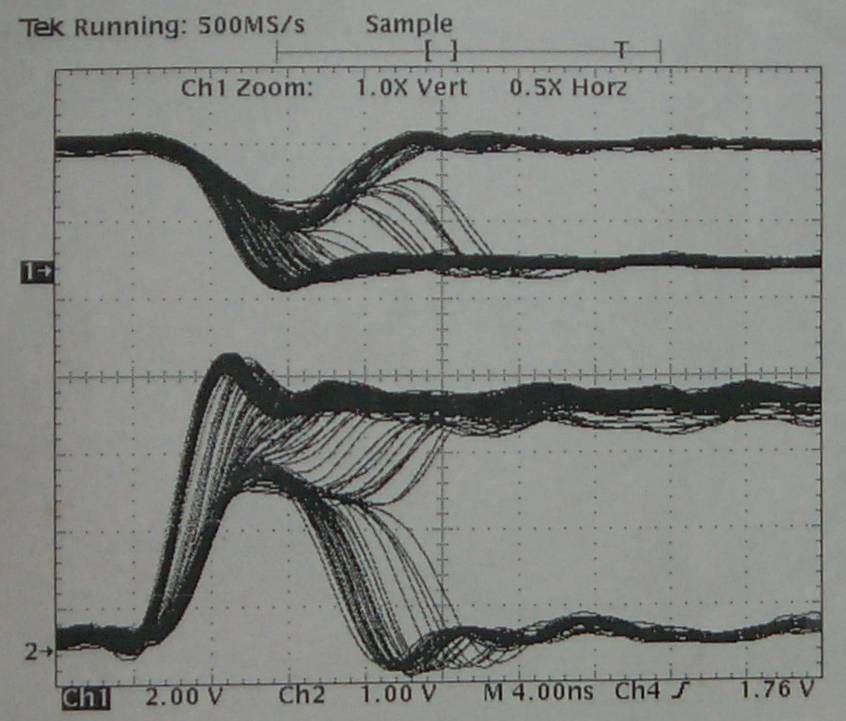
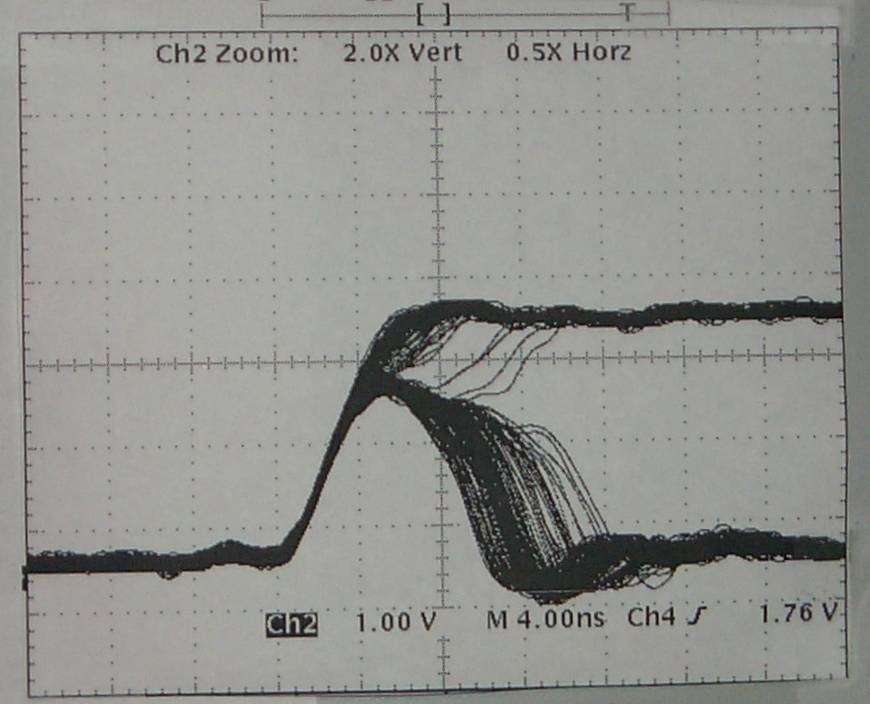
These are far from just delayed outputs! The end result though is still the same, systems that fail. But seeing these scope pictures of the actual Q output might make you think about how you measure metastability. For example, the lower trace on the first picture, the vertical scale is 1V per division, and the 0V level is 1/2 a division above the bottom of the screen. The horizontal scale is 4ns per division. Now what if your test system took a sample at 10ns, and used a threshold of 1.5 volts (2 div up from the bottom of the picture). You would say that the signal is always high at this point. If you sampled again at 20 ns (middle of the screen, you would say that it has resolved for all the traces shown, and you would count all the transitions that returned to ground (because they were high at 10ns). All those traces that ended up high would not be counted. This would be bad if in the real system the device listening to the DUT happened to have a threshold of 2.1 volts (right in the middle of that cute little hump). This also shows why using a signal like this as a clock could be a real disaster. Knowing what the trajectory of the DUT output looks like can make you think a lot harder about how you test it. > So, bearing this in mind, a thought experiment. We have an async >input, moving to a synchronising clock domain at (say) 1000MHz. Say we >have a budget of 5ns of latency to mitigate metastability. The sample >is captured after the metastability mitigation circuit (MMC) with a FF >called the output FF. > My first question is, which of these choices of MMC is least likely >to produce metastability at the output FF? >1) The MMC is a 4 FF long shift register clocked at 1000MHz. >MMC1 : process(clock) >begin > if rising_edge(clock) then > FF1 <= input; > FF2 <= FF1; > FF3 <= FF2; > FF4 <= FF3; > output <= FF4; > end if; >end process; Basically the improvement in MTBF is a function of the slack time you give it to resolve. This is the sum of the slack time between FF1 and FF2, FF2 and FF3, FF3 and FF4, and FF4 and output. Lets throw some numbers at it. Setup time is 75ps, clock to Q is 200ps, routing delay between any pair of Q to D paths is 100ps. Clock distribution skew is 25ps (in the unfortunate direction). So we have 4 paths of 1000ps - (75+200+100+25) = 4 * 600ps = 2.4ns >2) The MMC is 4 FFs, each clock enabled every second clock. >MMC2 : process(clock) >begin > if rising_edge(clock) then > toggle <= not toggle; > if toggle = '1' then > FF1 <= input; > FF3 <= FF1; > output <= FF3; > else > FF2 <= input; > FF4 <= FF2; > output <= FF4; > end if; > end if; >end process; Ok, so this is weird, and it adds a mux :-) Transit time through muxes is 200ps (assume that getting toggle to it is a non issue), and its output connects to the D of the output FF. No extra routing delay. Path 1: slack from FF1 to FF3 plus slack from FF3 to output 2000-(75+200+100+25)+2000-(75+200+100+25+200)= 3.0ns Path 2: same slacks, just different FFs 3.0ns So: weird but better :-) I could of course screw up the results by changing the delay numbers, but they are pretty realistic for current technology. > Option 1) offers extra stages of synchronization between the input >and output, but the 1ns gap between FFs means that metastability is >more likely to propagate. Option 2) waits 2ns for the sample FFs to >make up their mind, vastly decreasing the metastability probability. Yep. > My second question is, does the type of metastability, i.e. the >things in Philip's list, affect which is the better choice? For >instance, if the first FF in the MMC exhibits oscillations in >metastability, then the second FF in the MMC would have several >chances, as its input oscillates, to sample at the 'wrong' time. This >might favour MMC option 2). Actually MMC 2 is favored regardless of oscillations or not because of the 600ps of additional slack time. >If, however, the first FF in the MMC goes >into option 5) metastability, then there's only one chance for the >second FF to sample at the 'wrong' time. This might confer an >advantage on MMC option 1). My thinking on this has always been that the only thing that matters is the resolving time (slack) and the thought experiments about later stages sampling at just the right time to catch the previous FF resolving only cloud the issue. I am not as confident on this issue as I am on others though. What I am confident on though, is that there is a better MMC than your two, and it follows on from MMC #2. Just use 2 FFs, and clock them every 4 ns: (that is, enable them every 4th clock cycle. This would mean though that unlike MMC #2, which runs 2 parallel paths and avoids some latency, this could have upto 4 ns of extra latency, if you just miss the input change) slack from FF1 to output: 4000-(75+200+100+25) = 3.6ns If the latency is really a problem, you could build on the MMC #2 design and have 4 paths each out of phase by 1 clock cycle. Since the path is now only 2 FFs long you would have to have 4 output FFs, and the selector mux would be after these 4 FFs. On the bright side, the mux delay does not eat into the resolving slack time, but it would eat some of the available cycle time in the logic that follows the output FF. > > Anyway, I'm still thinking about this. I think the clock frequency >may decide which is better for a given FF type. Any comments? > Cheers, Syms. Thanks for an interesting question. Comments above :-)
=============================================================================
Philip Freidin
2003/09/01
Here is an excellent Metastability Bibliography
2004/08/01
Here is an excellent article on the system design aspects of signals
crossing clock domains by Roy H. Parker.
(There are some minor problems with the figure numbers in the text, which are off by one, but it is pretty obvious)
Here is an article, from Peter Alfke at Xilinx, published by EETimes network (sorry, link is broken, content no longer available)
Here is another article, from Peter Alfke at Xilinx (sorry, link is broken, content no longer available)
The thread that starts here describes a good synchronizer by Rick Collins that may be better than the one
presented by Roy Parker. (follow the thread by clicking the '>>' after the 'T' on the line that starts 'Links:')
2004/12/25
Here is a white paper from Cadence on Clock Domain Crossing
=============================================================================
Philip Freidin 2005/07/11 The following course at MIT contains a rather nice lecture on Synchronization, Metastability and Arbitration. The lecture presentation PDF is reproduced here with permission of the author, Steve Ward. The course material includes a quiz with answers. Here is a link to the quiz with the answers hidden until you ask for them. When I was reviewing the quiz, I found one error. I discussed it with the author and he agreed. It will be corrected in a future version. I leave it as an exercise for you to find the error :-) Philip Freidin 2010/02/19 Well, it's 4.5 years later, and the error is still there. Try and find it :-)